【数理统计】从头开始时间序列-Day1

【数理统计】从头开始时间序列-Day1
6Young为了应对即将到来的求职季,也为了巩固一波基础知识,我打算从头学习一下时间序列分析的基础知识。事实上我也没有真正系统地学习过,都是有基础的了解,然后随时使用,随时查找资料。这样的程度可是没有办法应付面试官的,静下心来开始吧!!!
首先,我们要了解时间序列分析过程中的一些基本用语,时间序列($X_t$)就是按时间顺序排列的随机变量序列。时间序列的观测样本($x_t$)就是对时间序列各随机变量的观测样本,一定是有限多个。时间序列的一次实现/一条轨道($X(t)$)是时间序列的一组实际观测。时间序列分析的任务($x(t)$)是对时间序列数据的建模,解释、控制或预报。
以上是对时间序列的基本了解,其他的专业术语我们随时遇到随时解释。
时间序列分解
时间序列分解是指将序列中的各个数据根据不同来源拆分成不同的数。通常我们会将一个序列分解为趋势项,季节项,随机项,有时还会有随机周期项
对于时间序列的固定的周期季节项$S(T)$,以及周期长度$s$我们进行如下假设:
$$
\forall t, S(t+s) = S(t)) \
\sum_{j=1}^sS_j = 0
$$
关于随机项$R_t$,可以假设:
$$
\forall t, E(R_t) = 0
$$
比如对于这样一个数据:
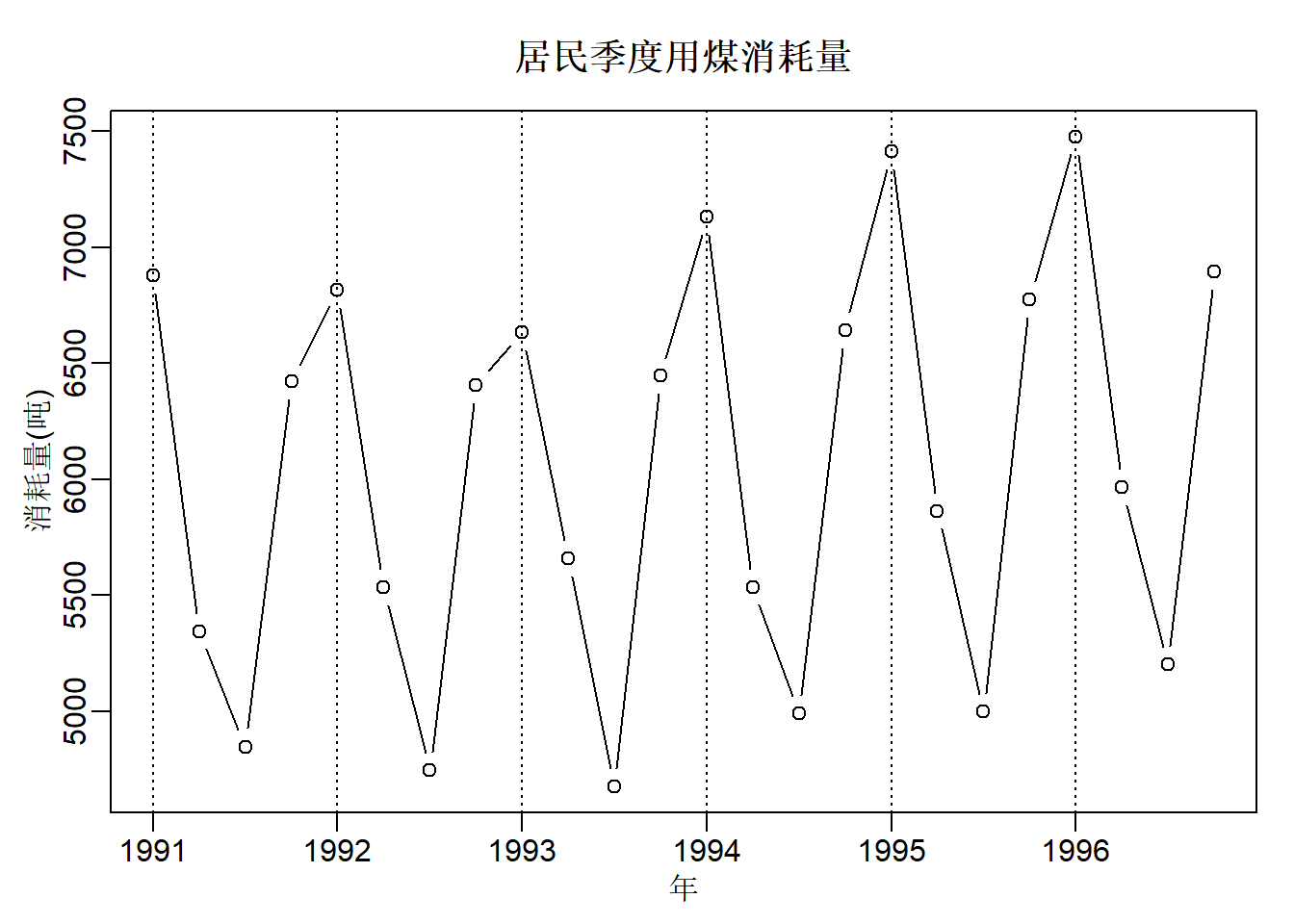
简单观察数据,我们可以明显看出序列存在一个向上增加的趋势,并且存在长度为4的周期。
趋势项估计
每年平均法:得知4季度,也就是一年为周期后,可以计算数据在一年中的平均值作为趋势项;
线性回归拟合:因为我们有季节项和随机项和为0的假设,因此可以直接对数据进行线性回归分析,拟合出一条直线作为趋势项;此外呢,我们也可以构建表示季度的虚拟变量,与元数据同时进行回归,直接计算得出趋势项与季度项
二次曲线回归:如果想更精细的分析趋势项,用二次曲线回归能更好的找出其中的非线性关系。
滑动平均估计:均线法是常用的估计趋势的方法,可以用等权的或者不等权的移动平均方法进行估计。
R语言实现
我们当然可以用上述的逻辑自己一步一步的对一个时间序列进行分解,好处在于可以随自己的需要选择合适的估计方案。除此以外呢,使用一个已经封装打包好的方法当然是最好的,R语言作为经济学中最常用的工具之一,给我们提供了大量的解决方案:
R的stats包的
decompose()函数输入一个时间序列, 将其分解为趋势项、季节项和随机项。 去趋势的方法是中心对称滑动平均。 可以用type="additive"或type="multiplicative"指定各项之间是相加还是相乘。考虑著名的美国泛美航空公司1949-1960 的国际航班订票数的月度数据(单位:千人),12年144个月的数据:1
plot(decompose(AirPassengers, type="multiplicative"))

滑动平均是平滑(smoothing)的一种, 中心对称的滑动平均会丢失序列开始和结束部分的若干点。 R的stats包提供了函数
stl(), 该函数基于loess局部加权回归估计季节项, 可以减少异常点的影响, 属于稳健回归。 用同月份(季度)的数值估计平滑的季节变动, 减去季节项后再用平滑方法估计趋势。 滑动平均和loess局部加权回归都不能表示成公式模型,平滑的另一说法是“滤波”。1
plot(stl(AirPassengers, s.window=3))

R的stats包的
StructTS()函数用状态空间模型表示时间序列分解, 用最大似然方法估计各个成分。 结果列表中的fitted有三列level,slope,sea。1
2
3
4
5
6res2 <- StructTS(log(AirPassengers), type="BSM")
res2b <- cbind(log(AirPassengers), fitted(res2), resid(res2))
colnames(res2b) <- c(
"Series", "level", "slope", "seasonal", "residual"
)
plot(res2b)
现在,我们就学会了时间序列分析中最基本的分析方法——时间序列的分解。
未完待续~~~






